空间复杂度¶
「空间复杂度 space complexity」用于衡量算法占用内存空间随着数据量变大时的增长趋势。这个概念与时间复杂度非常类似,只需将“运行时间”替换为“占用内存空间”。
算法相关空间¶
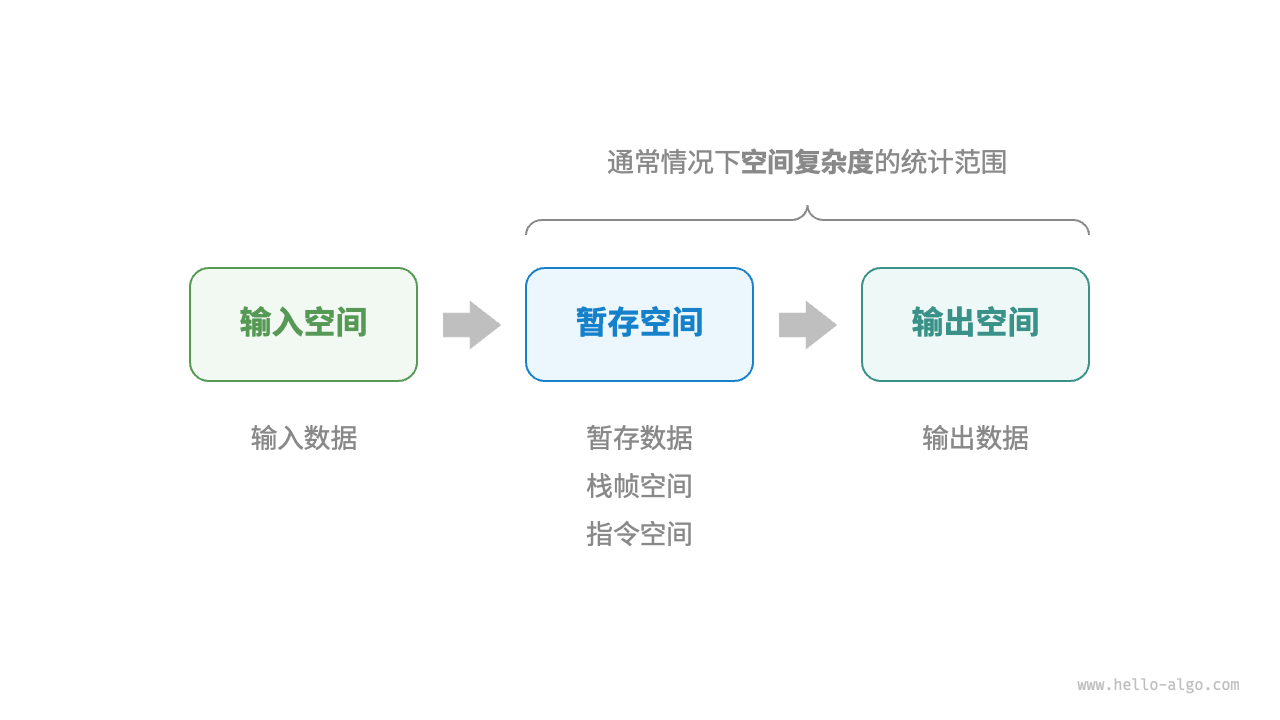
算法在运行过程中使用的内存空间主要包括以下几种。
- 输入空间:用于存储算法的输入数据。
- 暂存空间:用于存储算法在运行过程中的变量、对象、函数上下文等数据。
- 输出空间:用于存储算法的输出数据。
一般情况下,空间复杂度的统计范围是“暂存空间”加上“输出空间”。
暂存空间可以进一步划分为三个部分。
- 暂存数据:用于保存算法运行过程中的各种常量、变量、对象等。
- 栈帧空间:用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧,函数返回后,栈帧空间会被释放。
- 指令空间:用于保存编译后的程序指令,在实际统计中通常忽略不计。
在分析一段程序的空间复杂度时,我们通常统计暂存数据、栈帧空间和输出数据三部分,如下图所示。
相关代码如下:
class Node:
"""类"""
def __init__(self, x: int):
self.val: int = x # 节点值
self.next: Node | None = None # 指向下一节点的引用
def function() -> int:
"""函数"""
# 执行某些操作...
return 0
def algorithm(n) -> int: # 输入数据
A = 0 # 暂存数据(常量,一般用大写字母表示)
b = 0 # 暂存数据(变量)
node = Node(0) # 暂存数据(对象)
c = function() # 栈帧空间(调用函数)
return A + b + c # 输出数据
/* 结构体 */
struct Node {
int val;
Node *next;
Node(int x) : val(x), next(nullptr) {}
};
/* 函数 */
int func() {
// 执行某些操作...
return 0;
}
int algorithm(int n) { // 输入数据
const int a = 0; // 暂存数据(常量)
int b = 0; // 暂存数据(变量)
Node* node = new Node(0); // 暂存数据(对象)
int c = func(); // 栈帧空间(调用函数)
return a + b + c; // 输出数据
}
/* 类 */
class Node {
int val;
Node next;
Node(int x) { val = x; }
}
/* 函数 */
int function() {
// 执行某些操作...
return 0;
}
int algorithm(int n) { // 输入数据
final int a = 0; // 暂存数据(常量)
int b = 0; // 暂存数据(变量)
Node node = new Node(0); // 暂存数据(对象)
int c = function(); // 栈帧空间(调用函数)
return a + b + c; // 输出数据
}
/* 结构体 */
type node struct {
val int
next *node
}
/* 创建 node 结构体 */
func newNode(val int) *node {
return &node{val: val}
}
/* 函数 */
func function() int {
// 执行某些操作...
return 0
}
func algorithm(n int) int { // 输入数据
const a = 0 // 暂存数据(常量)
b := 0 // 暂存数据(变量)
newNode(0) // 暂存数据(对象)
c := function() // 栈帧空间(调用函数)
return a + b + c // 输出数据
}
/* 类 */
class Node {
var val: Int
var next: Node?
init(x: Int) {
val = x
}
}
/* 函数 */
func function() -> Int {
// 执行某些操作...
return 0
}
func algorithm(n: Int) -> Int { // 输入数据
let a = 0 // 暂存数据(常量)
var b = 0 // 暂存数据(变量)
let node = Node(x: 0) // 暂存数据(对象)
let c = function() // 栈帧空间(调用函数)
return a + b + c // 输出数据
}
/* 类 */
class Node {
val;
next;
constructor(val) {
this.val = val === undefined ? 0 : val; // 节点值
this.next = null; // 指向下一节点的引用
}
}
/* 函数 */
function constFunc() {
// 执行某些操作
return 0;
}
function algorithm(n) { // 输入数据
const a = 0; // 暂存数据(常量)
let b = 0; // 暂存数据(变量)
const node = new Node(0); // 暂存数据(对象)
const c = constFunc(); // 栈帧空间(调用函数)
return a + b + c; // 输出数据
}
/* 类 */
class Node {
val: number;
next: Node | null;
constructor(val?: number) {
this.val = val === undefined ? 0 : val; // 节点值
this.next = null; // 指向下一节点的引用
}
}
/* 函数 */
function constFunc(): number {
// 执行某些操作
return 0;
}
function algorithm(n: number): number { // 输入数据
const a = 0; // 暂存数据(常量)
let b = 0; // 暂存数据(变量)
const node = new Node(0); // 暂存数据(对象)
const c = constFunc(); // 栈帧空间(调用函数)
return a + b + c; // 输出数据
}
/* 类 */
class Node {
int val;
Node next;
Node(this.val, [this.next]);
}
/* 函数 */
int function() {
// 执行某些操作...
return 0;
}
int algorithm(int n) { // 输入数据
const int a = 0; // 暂存数据(常量)
int b = 0; // 暂存数据(变量)
Node node = Node(0); // 暂存数据(对象)
int c = function(); // 栈帧空间(调用函数)
return a + b + c; // 输出数据
}
use std::rc::Rc;
use std::cell::RefCell;
/* 结构体 */
struct Node {
val: i32,
next: Option<Rc<RefCell<Node>>>,
}
/* 创建 Node 结构体 */
impl Node {
fn new(val: i32) -> Self {
Self { val: val, next: None }
}
}
/* 函数 */
fn function() -> i32 {
// 执行某些操作...
return 0;
}
fn algorithm(n: i32) -> i32 { // 输入数据
const a: i32 = 0; // 暂存数据(常量)
let mut b = 0; // 暂存数据(变量)
let node = Node::new(0); // 暂存数据(对象)
let c = function(); // 栈帧空间(调用函数)
return a + b + c; // 输出数据
}
推算方法¶
空间复杂度的推算方法与时间复杂度大致相同,只需将统计对象从“操作数量”转为“使用空间大小”。
而与时间复杂度不同的是,我们通常只关注最差空间复杂度。这是因为内存空间是一项硬性要求,我们必须确保在所有输入数据下都有足够的内存空间预留。
观察以下代码,最差空间复杂度中的“最差”有两层含义。
- 以最差输入数据为准:当 \(n < 10\) 时,空间复杂度为 \(O(1)\) ;但当 \(n > 10\) 时,初始化的数组
nums占用 \(O(n)\) 空间,因此最差空间复杂度为 \(O(n)\) 。 - 以算法运行中的峰值内存为准:例如,程序在执行最后一行之前,占用 \(O(1)\) 空间;当初始化数组
nums时,程序占用 \(O(n)\) 空间,因此最差空间复杂度为 \(O(n)\) 。
在递归函数中,需要注意统计栈帧空间。观察以下代码:
函数 loop() 和 recur() 的时间复杂度都为 \(O(n)\) ,但空间复杂度不同。
- 函数
loop()在循环中调用了 \(n\) 次function(),每轮中的function()都返回并释放了栈帧空间,因此空间复杂度仍为 \(O(1)\) 。 - 递归函数
recur()在运行过程中会同时存在 \(n\) 个未返回的recur(),从而占用 \(O(n)\) 的栈帧空间。
常见类型¶
设输入数据大小为 \(n\) ,下图展示了常见的空间复杂度类型(从低到高排列)。
常数阶 \(O(1)\)¶
常数阶常见于数量与输入数据大小 \(n\) 无关的常量、变量、对象。
需要注意的是,在循环中初始化变量或调用函数而占用的内存,在进入下一循环后就会被释放,因此不会累积占用空间,空间复杂度仍为 \(O(1)\) :
线性阶 \(O(n)\)¶
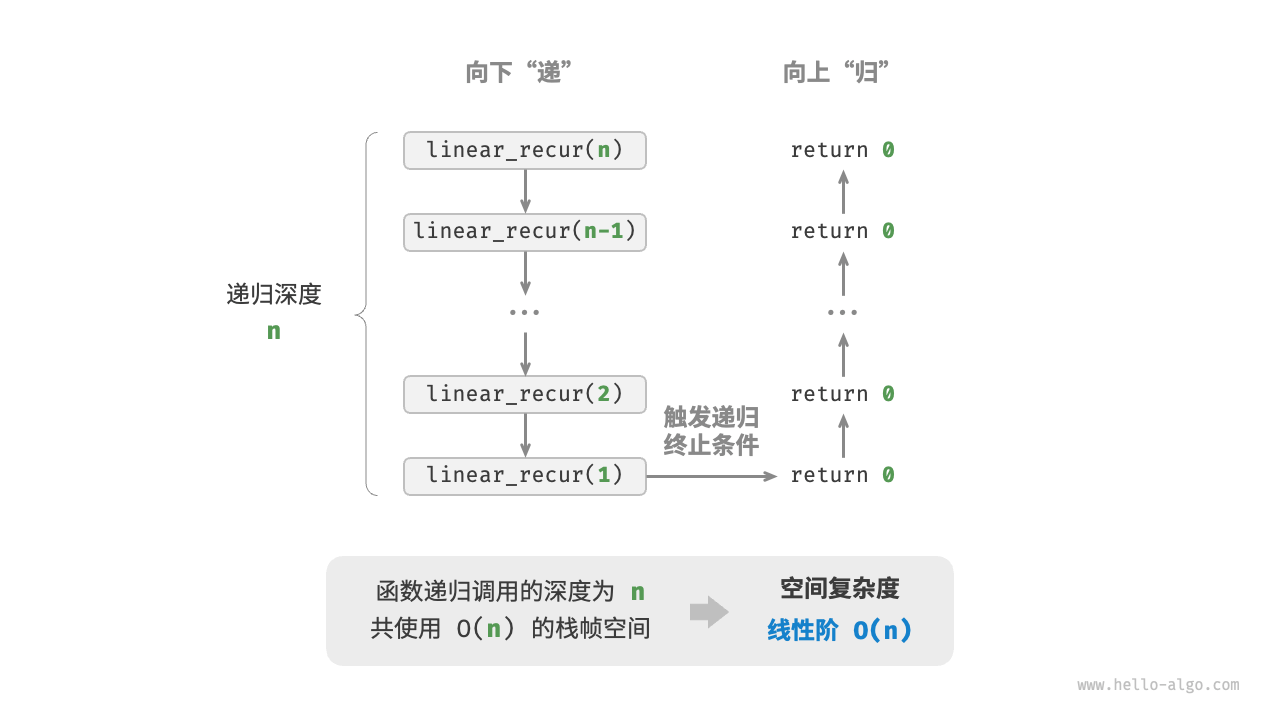
线性阶常见于元素数量与 \(n\) 成正比的数组、链表、栈、队列等:
如下图所示,此函数的递归深度为 \(n\) ,即同时存在 \(n\) 个未返回的 linear_recur() 函数,使用 \(O(n)\) 大小的栈帧空间:
平方阶 \(O(n^2)\)¶
平方阶常见于矩阵和图,元素数量与 \(n\) 成平方关系:
如下图所示,该函数的递归深度为 \(n\) ,在每个递归函数中都初始化了一个数组,长度分别为 \(n\)、\(n-1\)、\(\dots\)、\(2\)、\(1\) ,平均长度为 \(n / 2\) ,因此总体占用 \(O(n^2)\) 空间:
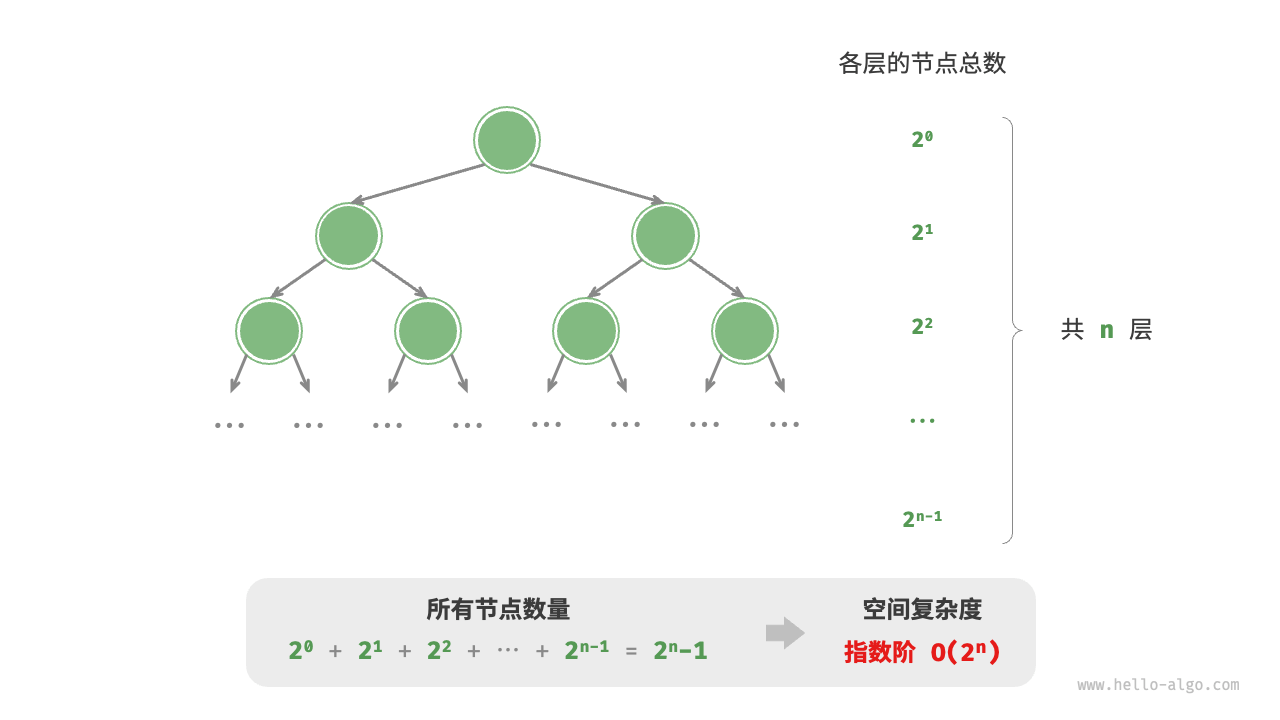
指数阶 \(O(2^n)\)¶
指数阶常见于二叉树。观察下图,层数为 \(n\) 的“满二叉树”的节点数量为 \(2^n - 1\) ,占用 \(O(2^n)\) 空间:
对数阶 \(O(\log n)\)¶
对数阶常见于分治算法。例如归并排序,输入长度为 \(n\) 的数组,每轮递归将数组从中点处划分为两半,形成高度为 \(\log n\) 的递归树,使用 \(O(\log n)\) 栈帧空间。
再例如将数字转化为字符串,输入一个正整数 \(n\) ,它的位数为 \(\lfloor \log_{10} n \rfloor + 1\) ,即对应字符串长度为 \(\lfloor \log_{10} n \rfloor + 1\) ,因此空间复杂度为 \(O(\log_{10} n + 1) = O(\log n)\) 。
权衡时间与空间¶
理想情况下,我们希望算法的时间复杂度和空间复杂度都能达到最优。然而在实际情况中,同时优化时间复杂度和空间复杂度通常非常困难。
降低时间复杂度通常需要以提升空间复杂度为代价,反之亦然。我们将牺牲内存空间来提升算法运行速度的思路称为“以空间换时间”;反之,则称为“以时间换空间”。
选择哪种思路取决于我们更看重哪个方面。在大多数情况下,时间比空间更宝贵,因此“以空间换时间”通常是更常用的策略。当然,在数据量很大的情况下,控制空间复杂度也非常重要。