堆排序¶
Tip
阅读本节前,请确保已学完“堆“章节。
「堆排序 heap sort」是一种基于堆数据结构实现的高效排序算法。我们可以利用已经学过的“建堆操作”和“元素出堆操作”实现堆排序。
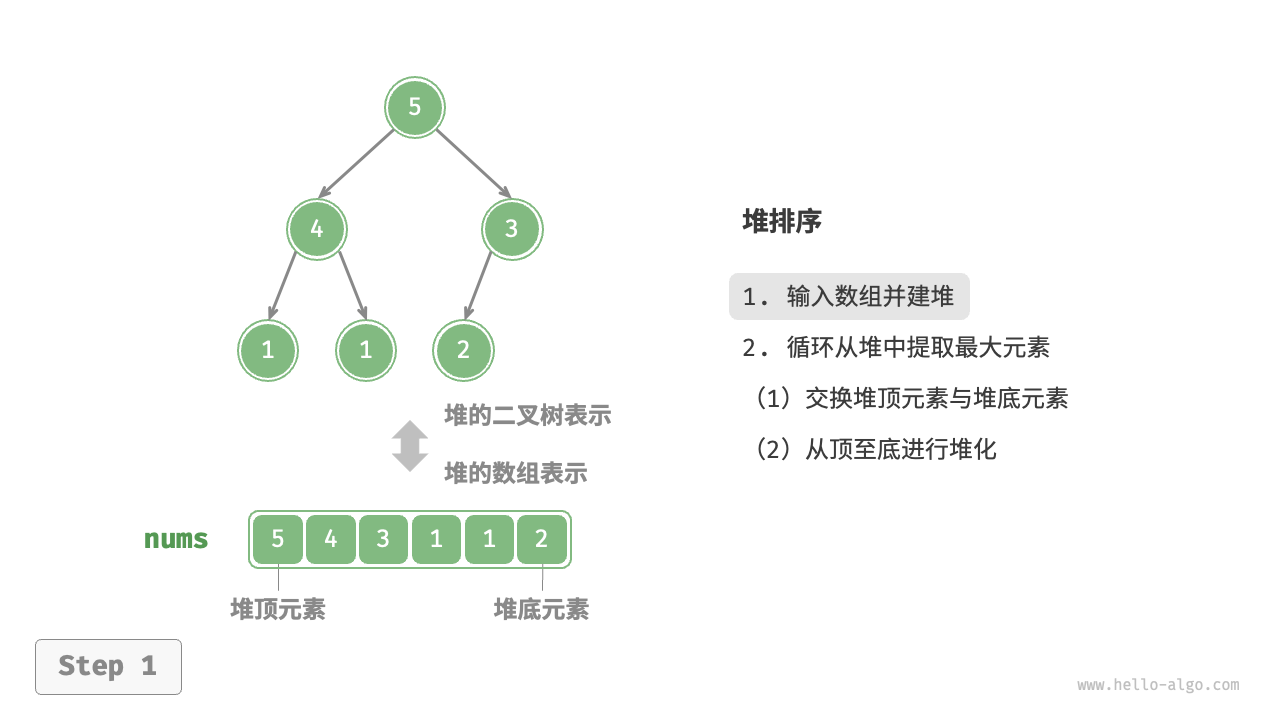
- 输入数组并建立小顶堆,此时最小元素位于堆顶。
- 不断执行出堆操作,依次记录出堆元素,即可得到从小到大排序的序列。
以上方法虽然可行,但需要借助一个额外数组来保存弹出的元素,比较浪费空间。在实际中,我们通常使用一种更加优雅的实现方式。
算法流程¶
设数组的长度为 \(n\) ,堆排序的流程如下图所示。
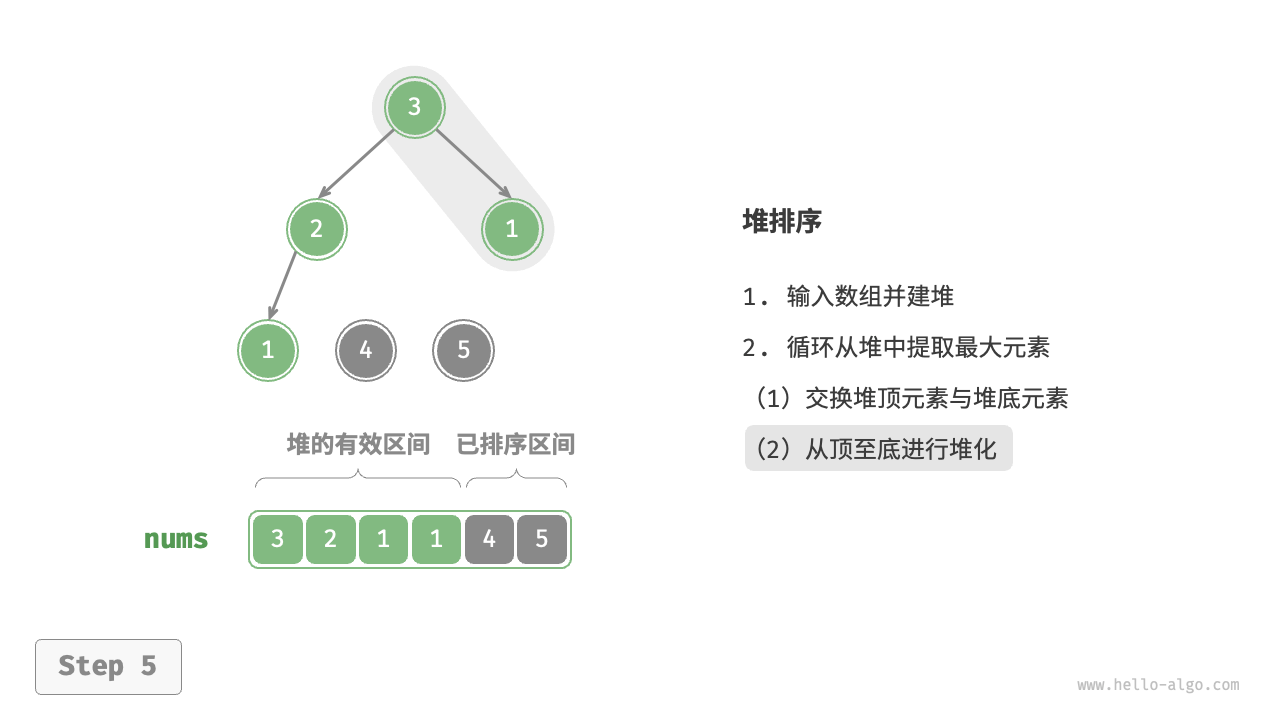
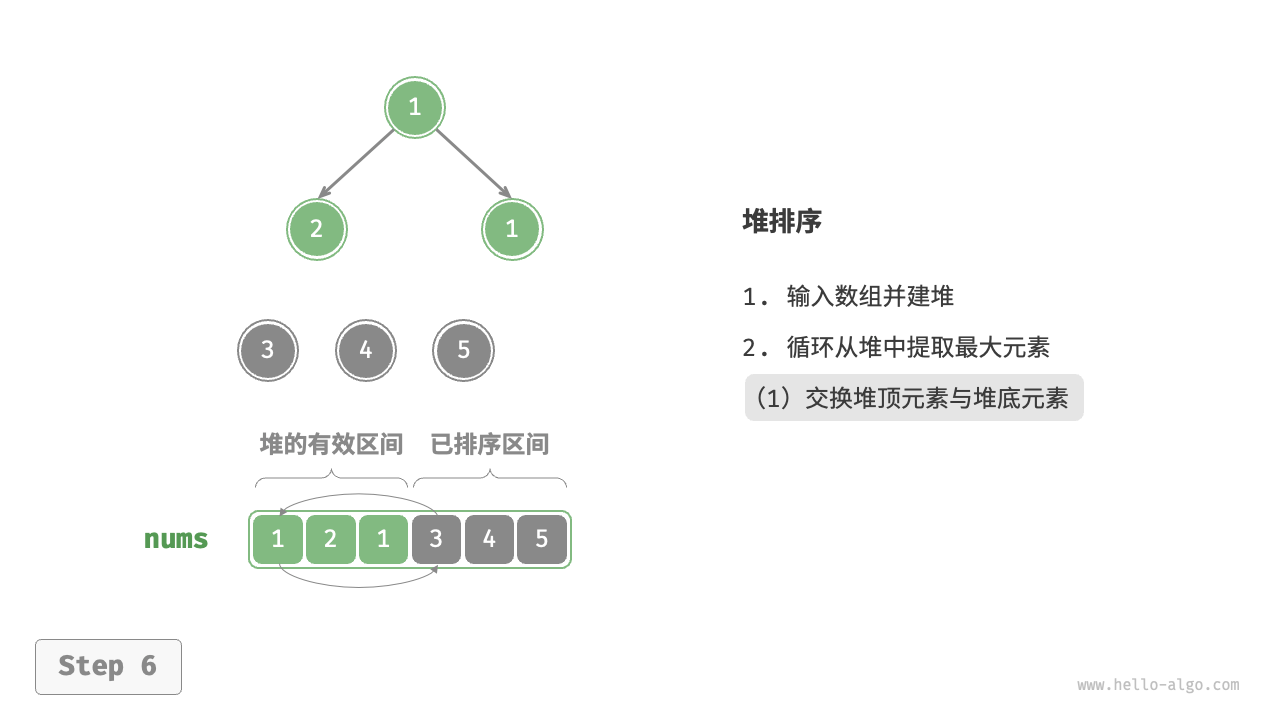
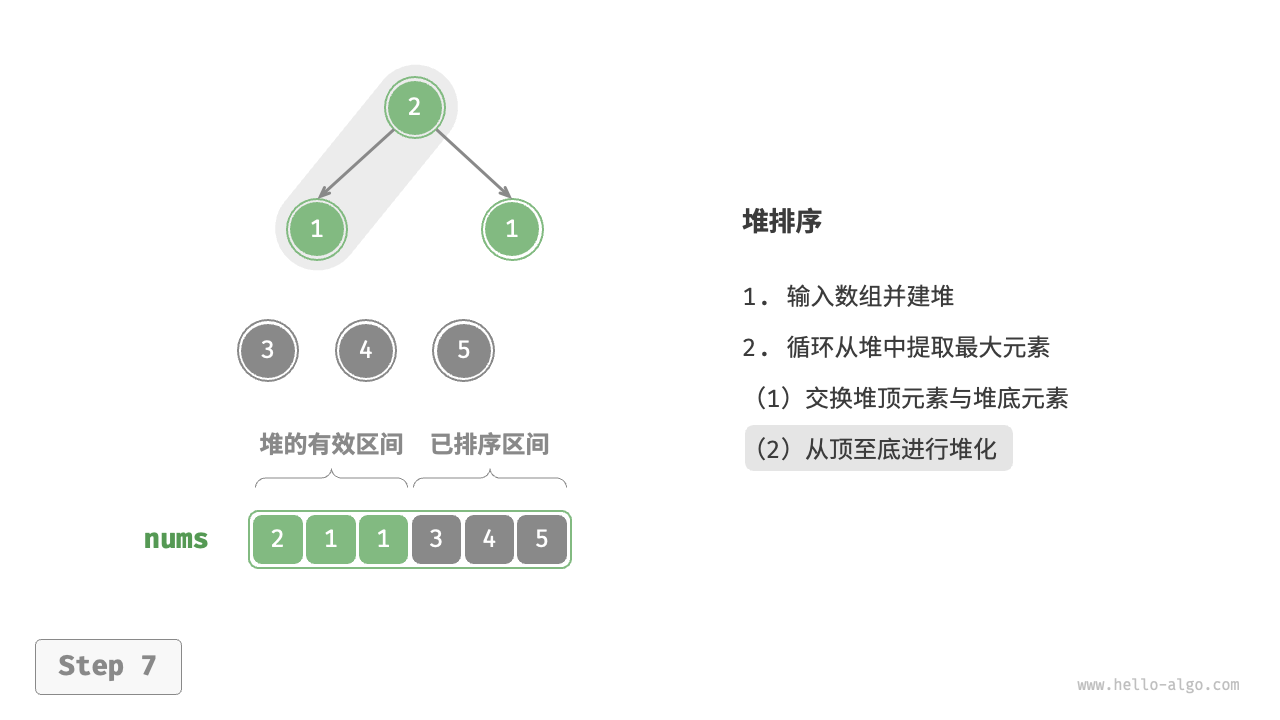
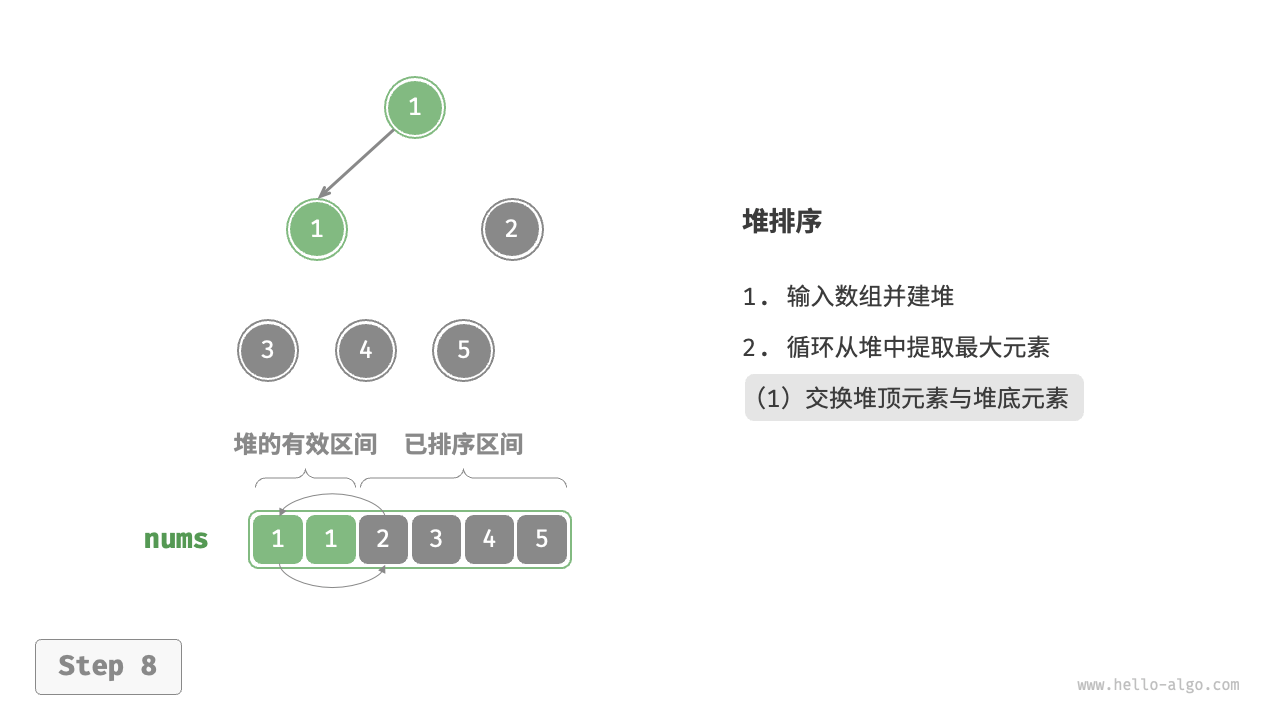
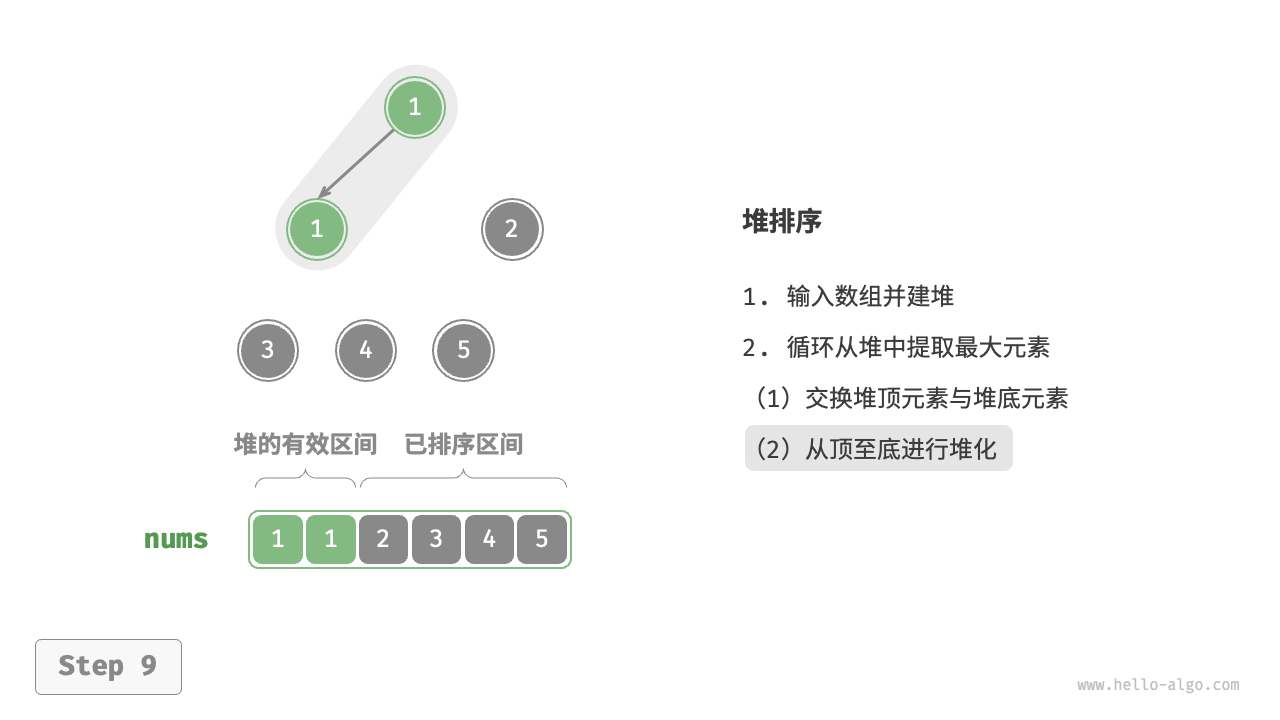
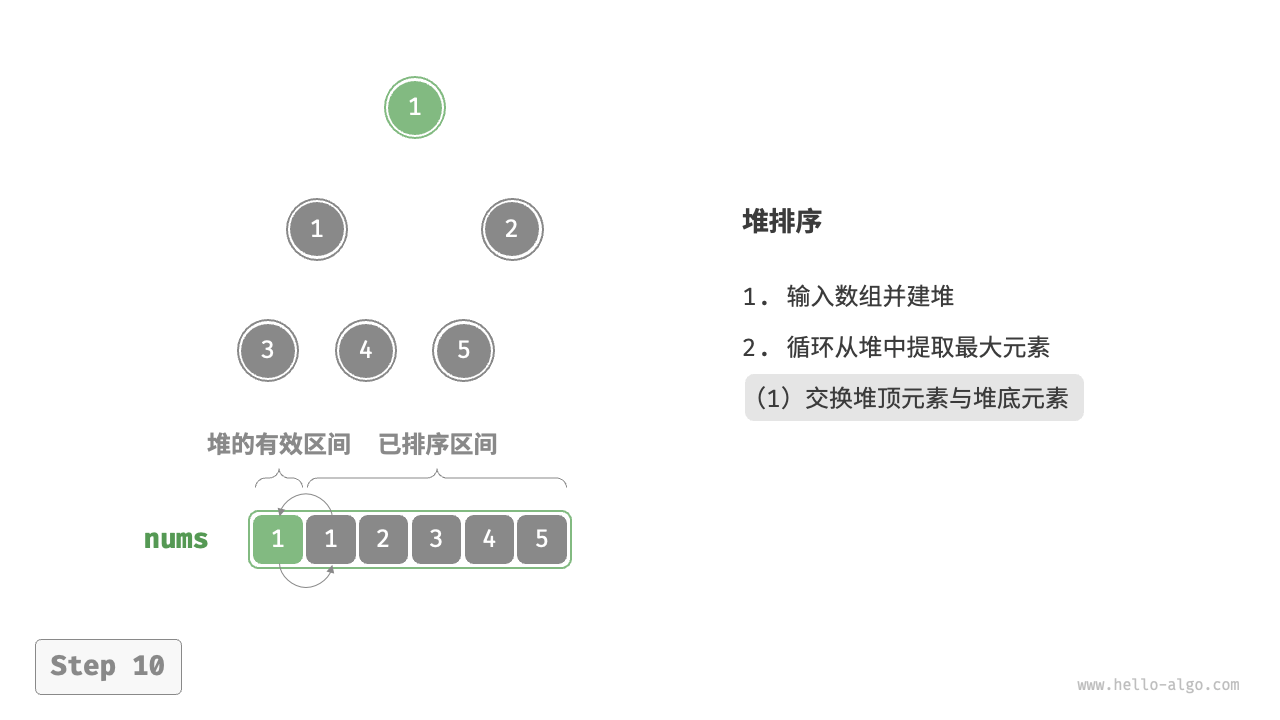
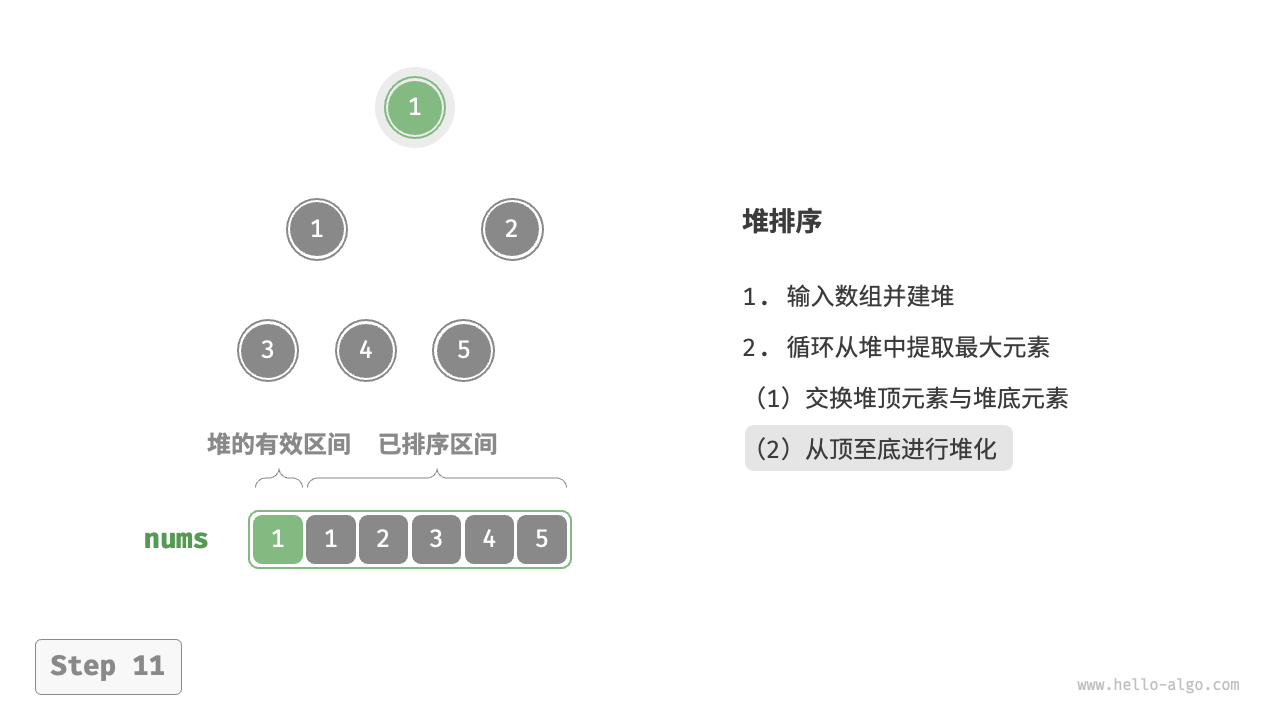
- 输入数组并建立大顶堆。完成后,最大元素位于堆顶。
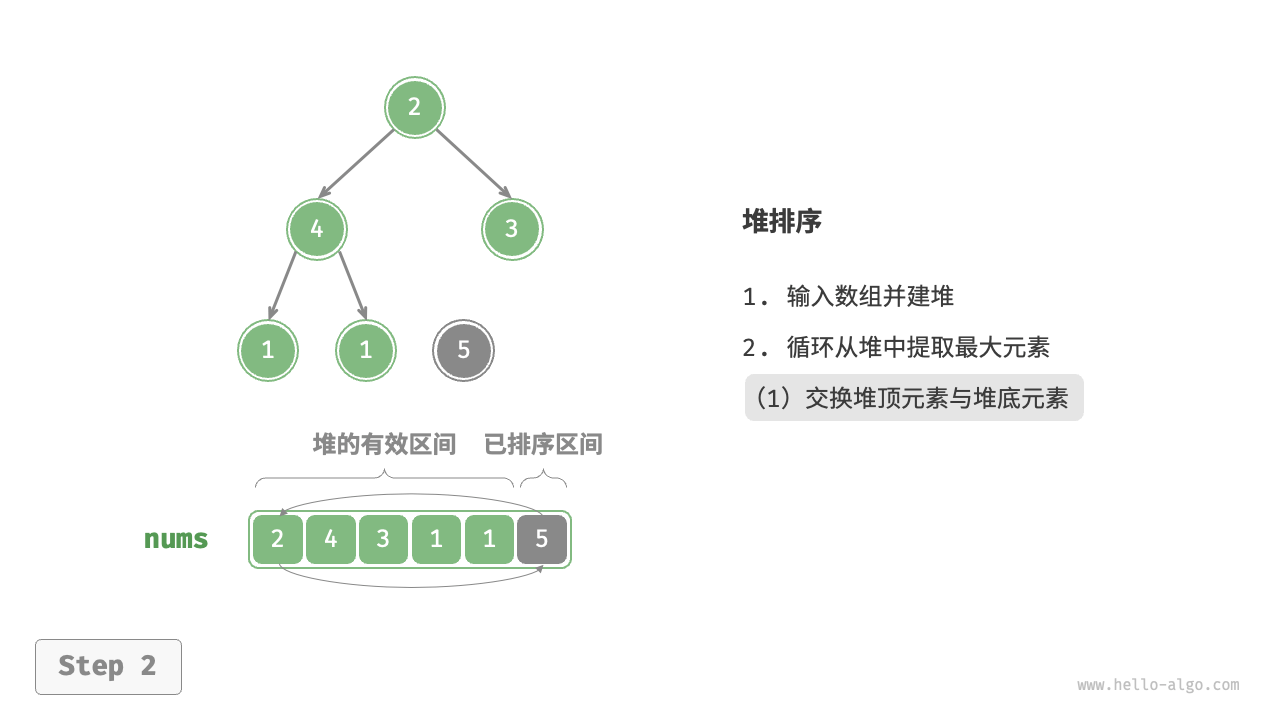
- 将堆顶元素(第一个元素)与堆底元素(最后一个元素)交换。完成交换后,堆的长度减 \(1\) ,已排序元素数量加 \(1\) 。
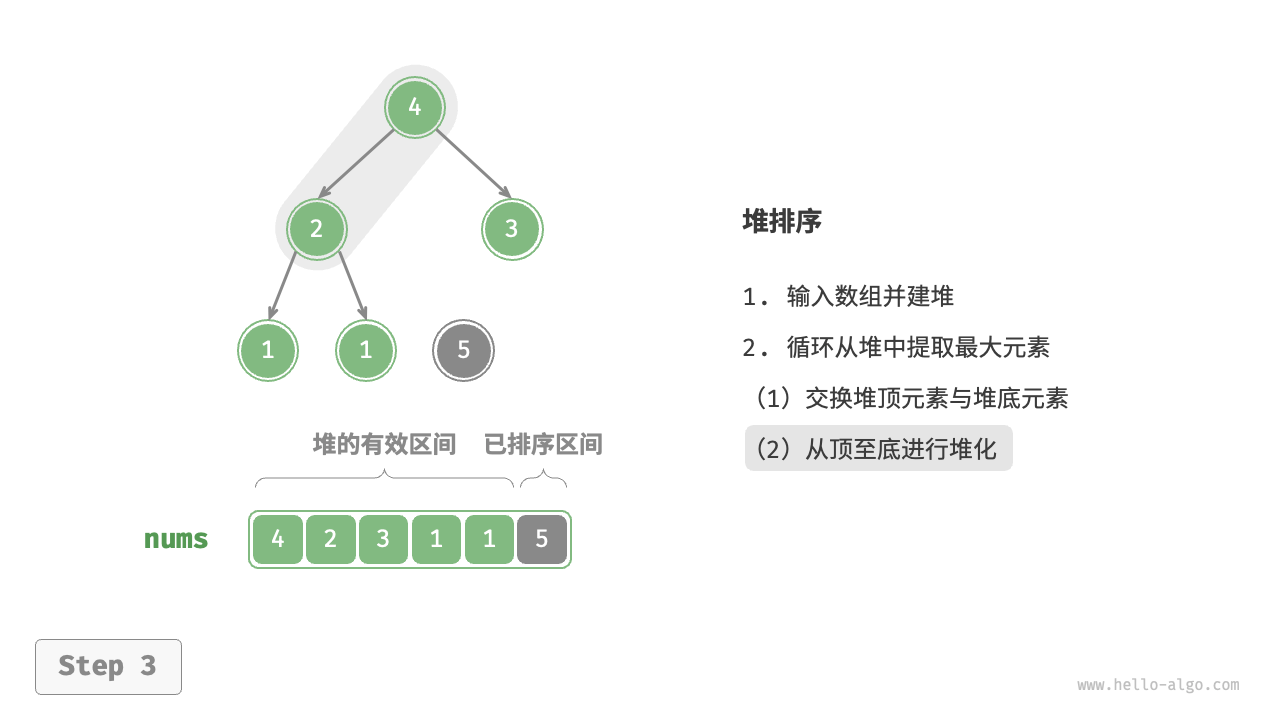
- 从堆顶元素开始,从顶到底执行堆化操作(sift down)。完成堆化后,堆的性质得到修复。
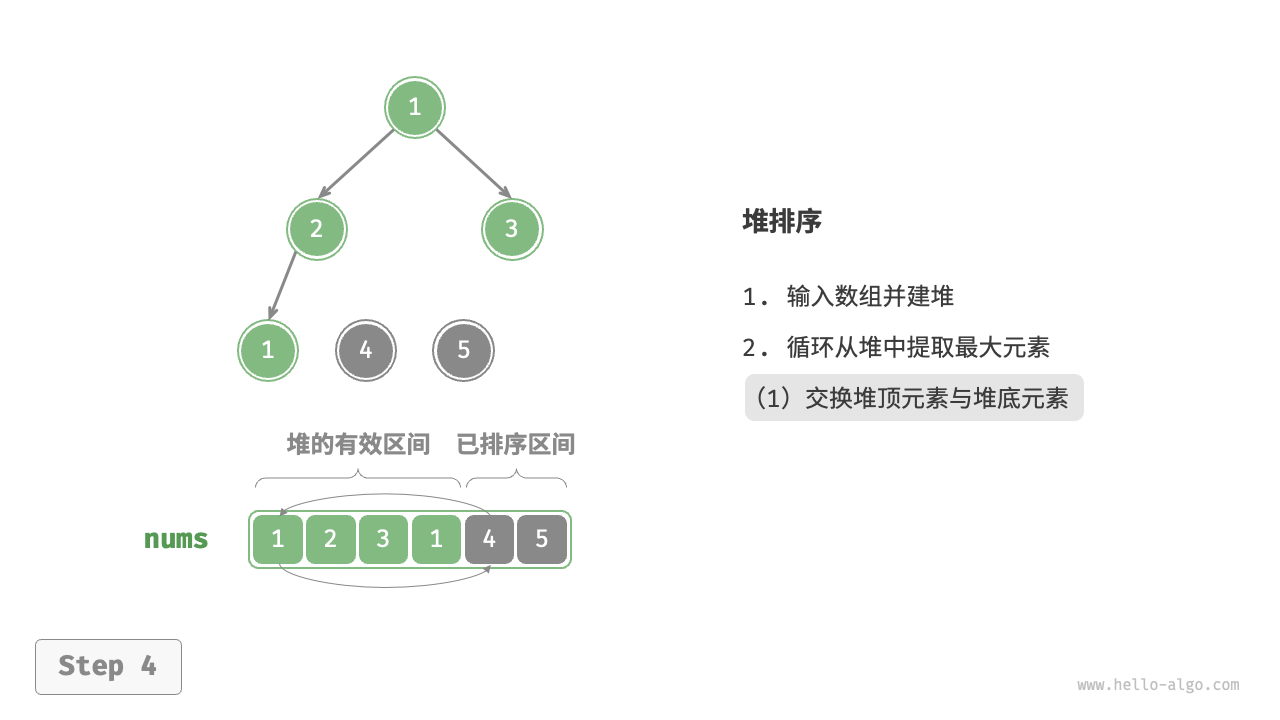
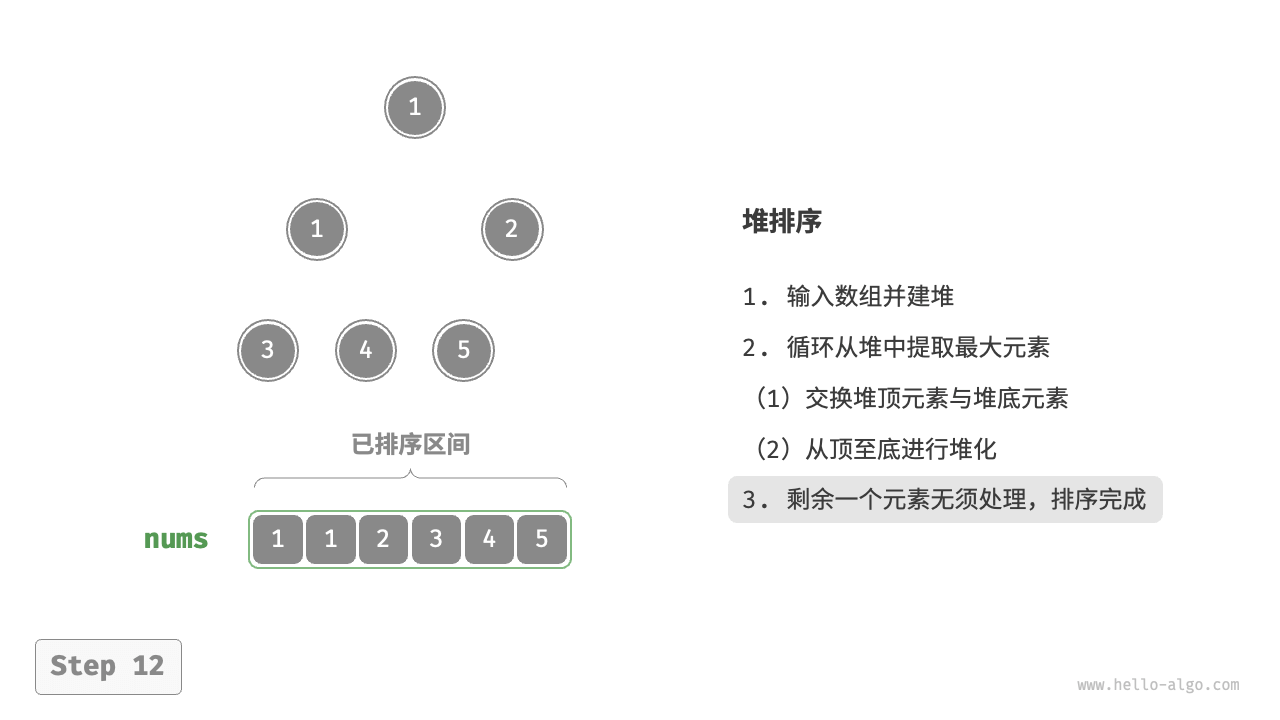
- 循环执行第
2.步和第3.步。循环 \(n - 1\) 轮后,即可完成数组排序。
Tip
实际上,元素出堆操作中也包含第 2. 步和第 3. 步,只是多了一个弹出元素的步骤。
在代码实现中,我们使用了与“堆”章节相同的从顶至底堆化 sift_down() 函数。值得注意的是,由于堆的长度会随着提取最大元素而减小,因此我们需要给 sift_down() 函数添加一个长度参数 \(n\) ,用于指定堆的当前有效长度。代码如下所示:
算法特性¶
- 时间复杂度为 \(O(n \log n)\)、非自适应排序:建堆操作使用 \(O(n)\) 时间。从堆中提取最大元素的时间复杂度为 \(O(\log n)\) ,共循环 \(n - 1\) 轮。
- 空间复杂度为 \(O(1)\)、原地排序:几个指针变量使用 \(O(1)\) 空间。元素交换和堆化操作都是在原数组上进行的。
- 非稳定排序:在交换堆顶元素和堆底元素时,相等元素的相对位置可能发生变化。